Heap Sort

⚠️ This post was created when I was in high school and is no longer maintained.

1. Tree properties

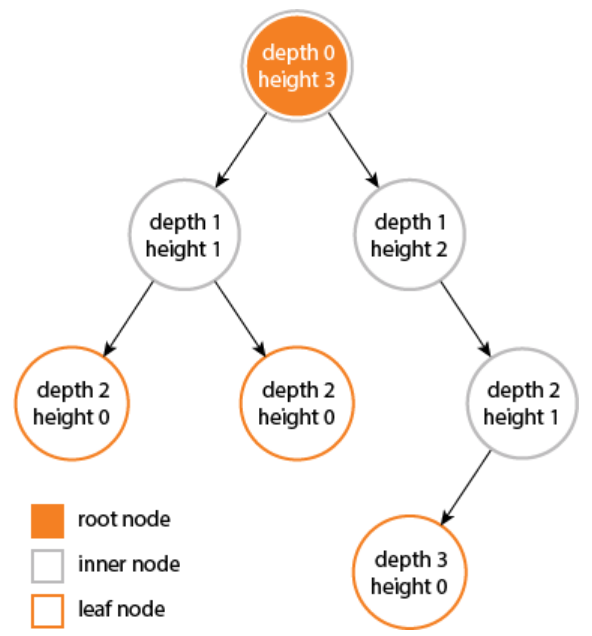
1. The depth of a node is the number of edges from the node to the tree’s root node. A root node will have a depth of 0.

2. The height of a node is the number of edges on the longest path from the node to a leaf. A leaf node will have a height of 0.

3. The height of a tree is the height of the root or the maximal depth. (For a complete binary tree, its height is Θ(lgn) )

4. A level or layer of a tree consists of all nodes of the same depth the number of levels is the height of the tree + 1

2. CLRS tips

(1) Key assumption

Assume that the trees rooted at left(i) and right(i) are max-heaps

In my point of view, we can assume that the max-heap is already created. We only need to build the heap once and use it to do other operations, which will comply with the assumption.

(2)

The children’s subtrees each have size at most $2n/3$ — the worst case occurs when the bottom level of the tree is exactly half-full and therefore we can describe the running time of MAX-HEAPIFY by the recurrence: $T(n) \leq T(2n/3) + \Theta(1)$

the worst-case scenario is when the bottom level is half-full:

(Intuition: an excellent answer form Quora)

Firstly, we assume that the lemma is true that the worst case occurs when the second last level is half-full. Let $T$ be a tree with a total number of node $N$. Suppose there are $k$ nodes at the second last level, then $k/2$ of them will have leaves. Thus, we have the following

#leaves at the last level == #nodes at the second last level

Now, we can consider that the $T$ consists of four parts:

1. the left subtree without the last level: $(k-1)$ nodes;
2. the right subtree: $(k-1)$ nodes;
3. the leaves at the last level of the left subtree: $k$ nodes;
4. the root node: 1; Tips:
   #nodes in a completely filled binary tree = (2 * #nodes at last level)-1 -> Geometric Progression $k-1 = 2(k/2) - 1$*

Hence, we have $k−1+k−1+k+1=n$ and so $3k=n−1$

Thus, the worst-case scenario occurs when the maximum heapify runs on the root node and then progresses to the leaves at the last level of the left subtree. Hence, the total number of nodes covered in the left subtree (including the last level) is

\[(k-1) + k + 1 = 2k = 2(n-1)/3 < 2n/3\]

(the size of the subtree is bounded by 2n/3)

In a nutshell, the time complexity of max-heapify is determined by the longest path from the root towards leaves. Suppose we have leaves more than half in the last row of T. Then the three components that we said were almost equal (left subtree without leaves, right subtree, leaves at the last level) will not be the case. In other words, the 3rd component would be larger. Consequently, the left subtree (including the leaves at last level) would be less than (2∗n/3) since some amount of this fraction is spread in the leaves in the right subtree at the last level. As a result, the longest path from the root towards the leaves becomes shorter.

• The maximal size of a subtree is $2n/3$:

(The number of nodes in the tree = 1 + (Number of nodes in Left Subtree) + (Number of nodes in Right Subtree))

The worst case scenario – assume that we have a tree that has last level half full with N nodes. The left subree is of height (h+1) and the right subtree is of height h.

• The number of nodes in the subtree: \(\begin{array}{c} N_{\text {left}}=1+2+4+8 \ldots+2^{h+1}=2^{h+2}-1 \mapsto(1) \\ N_{\text {right }}=1+2+4+8 \ldots+2^{h}=2^{h+1}-1\ \mapsto(2) \end{array}\)

• The total number of nodes in the tree: \(\begin{aligned} N &=N_{l e f t}+N_{r i g h t}+1 \\ &=1+3 *\left(2^{h+1}\right)-2 \end{aligned}\)

$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\downarrow$

\[2^{h+1}=(N+1) / 3\]

plugin this into (1)

\[\rightarrow N_{l e f t}=(n+1) / 3-1<\mathbf{2 n} / \mathbf{3}\]

(3)

the elements in the subarray $A[(⌊2/n⌋+1), (⌊2/n⌋+2),…,n]$ are all leaves of the tree, and so each is a 1-element heap, to begin with.

• $A[1, 2, …, ⌊2/n⌋ ]$: internal nodes
• $A[(⌊2/n⌋+1), (⌊2/n⌋+2),…,n]$: leaves (trivial max heaps)

3.Pseudocode

Sorting Strategy:

1. Build Max Heap from unordered array;
2. Find maximum element A[1];
3. Swap elements A[n] and A[1]: now max element is at the end of the array!
4. Discard node n from heap (by decrementing heap-size variable)
5. New root may violate max heap property, but its children are max heaps. Run max_heapify to fix this.
6. Go to Step 2 unless heap is empty.

---

Intuition

Each time, we extract the root of the max-heap, which will break the max-heap property, and rebuild the max-heap again.

algorithm HeapSort(array):
    BuildMaxHeap(array) --> built the initial max-heap
    heap_size = array.len
    For i = array.len downto 2 do
        exchange array[i] with array[1]
        heap_size -= 1
        MaxHeapify(array, 1) --> restore max-heap property

function LeftNode(i):
    return i * 2    --> if the indices contain 0, then we should impement a special case for it 

function RightNode(i):
    return i * 2 + 1

function ParentNode(i):
    return ⌊i/2⌋

function MaxHeapify(array, i):
    left_i  = LeftNode(i)
    right_i = RightNode(i)
    
    -- be careful that the boundary here is heap_size rather than an array.len --
    -- (so I think implementing a heap class is a good one so that we don't need to pass heap_size argument all the time) --
    if left_i ≤ heap_size and array[left_i] > array[i] then
        largest = left_i
    else
        largest = i
    
    --> be careful that here we compare right_i with largest!
    if right_i ≤ heap_size and array[right_i] > array[largest] then
        largest = right_i
        
    if largest != i then
        exchang array[i] with array[largest]
        MaxHeapify(array, largest)

function BuildMaxHeap(array):
    heap_size = array.len
    For i = ⌊array.len/2⌋ downto 1 do --why take floor()?
        MaxHeeapify(array, i)

---

4. Time Complexity

1. MaxHeapify() : describe by recurrence and calculate by master theorem (Theorem 4.1) \(T(n) = T(2n/3) + \Theta(1) = O(\log_2n)\) Tips: The running time of MaxHeapify() on a node of height $h$ is $O(h)$.

2. BuildMaxHeap() :

(1) Upper bound: \(\bigg(n~times~call~MaxHeapify()\bigg) * T\bigg(MaxHeapify()\bigg) \\ = O(n) * O(log_2n) = O(nlgn)\)

(2) Tighter bound (not asymptotically tight):

We can derive a tighter bound by observing that the time for MAX-HEAPIFY to run at a node varies with the height of the node in the tree, and the heights of most nodes are small.

Observe however that Max_Heapify takes O(1) for time for nodes that are one level above the leaves, and in general, O(l) for the nodes that are l levels above the leaves. We have n/4 nodes with level 1, n/8 with level 2, and so on till we have one root node that is lgn levels above the leaves.

Our tighter analysis relies on two properties: In any n-element heap:

• The heap has height ⌊lgn⌋;
• there are at most ⌈n/2^h+1^ ⌉ nodes of height h;

1. All in all:

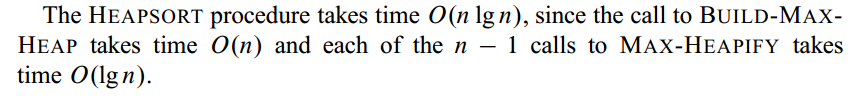
5. Space complexity

Heap sort is an in-place sorting algorithm.

4. Code

import scala.math._

class MaxHeap(val array: Array[Double]) {
    var _size:Int = array.length
    var _array:Array[Double]= array

    def leftNode(i: Int): Int = {
        if (i == 0) {
            return 1;
        } else {
            return i * 2;
        }
    }

    def rightNode(i: Int): Int = {
        if (i == 0) {
            return 2;
        } else {
            return i * 2 + 1;
        }
    }

    def maxHeapify(i: Int) {
        var left_i : Int = leftNode(i)
        var right_i: Int = rightNode(i)
        var largest = i

        if (left_i < _size && _array(left_i) > _array(i)) {
            largest = left_i
        }
        if (right_i < _size && _array(right_i) > _array(largest)) {
            largest = right_i
        }
        if (largest != i) {
            var tmp = 0.0
            tmp = _array(largest)
            _array(largest) = _array(i)
            _array(i) = tmp

            maxHeapify(largest)
        }
    }

    def buildMaxHeap() {
        var i: Int = 0
        for(i <- (floor(_size / 2)).asInstanceOf[Int] to 0 by -1) {
            maxHeapify(i)
        }
    }

    def heapSort() {
        buildMaxHeap()

        val i: Int = 0
        for (i <- (_array.length-1) to 1 by -1) {
            var tmp = 0.0
            tmp = _array(i)
            _array(i) = _array(0)
            _array(0) = tmp

            _size -= 1
            maxHeapify(0)
        }
    }
}

object HeapSortAlgo {
    def main(args: Array[String]): Unit = {
        var array = Array(4234,234234,23,234,-134,4123,41,578,-342,55,0.2323,0.325)
        val maxHeap = new MaxHeap(array)
        println("\nBefore sorting:")
        println(maxHeap._array.deep.mkString(" "))
        maxHeap.heapSort()
        println("\nAfter sorting:")
        println(maxHeap._array.deep.mkString(" "))
    } 
}

# Python
import math

class MaxHeap:
    def __init__(self, array):
        self.array = array
        self.size = len(array)

    def _left_node_(self, i):   
        if i == 0:
            return 1
        else:
            return i * 2

    def _right_node_(self, i):
        if i == 0:
            return 2
        else:
            return i * 2 + 1

    def _parent_node_(self, i):
        return math.floor(i / 2)

    def _max_heapify_(self, i):
        left_i  = self._left_node_(i)
        right_i = self._right_node_(i)

        if left_i < self.size and self.array[i] < self.array[left_i]:
            largest = left_i
        else:
            largest = i
        
        if right_i < self.size and self.array[largest] < self.array[right_i]:
            largest = right_i
        
        if largest != i:
            self.array[i], self.array[largest] = self.array[largest], self.array[i]
            self._max_heapify_(largest)
        
    def _build_max_heap_(self):
        for i in range(math.floor(self.size / 2), -1, -1):
            self._max_heapify_(i)

    def heap_sort(self):
        self._build_max_heap_() # build the initial max-heap
        for i in range(len(self.array)-1, 0, -1):
            self.array[i], self.array[0] = self.array[0], self.array[i]
            self.size -= 1
            print("Sorting: ", self.array)
            self._max_heapify_(0)

    
if __name__ == "__main__":
    # array = [4234,234234,23,234,-134,123,41,578,-342,55,0.9323,0.325]
    array = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
    max_heap = MaxHeap(array)
    print("Before sorting: ", max_heap.array)
    max_heap.heap_sort()
    print("After sorting:  ", max_heap.array)