Huffman Encoding
Updated:
⚠️ This post was created when I was in high school and is no longer maintained.
Huffman codes compress data very effectively: savings of 20% to 90% are typical, depending on the characteristics of the data being compressed. We consider the data to be a sequence of characters. Huffman’s greedy algorithm uses a table giving how often each character occurs (i.e., its frequency) to build up an optimal way of representing each character as a binary string. —— CRLS
1. Encode and Decode

1.1 Binary character code
Each character is represented by a unique binary string, which we call a codeword.
1.2 Fixed-/variable-length codeword
Say, a data file of 100,000 characters contains only the characters a~f, with the frequencies indicated.
- If we use a fixed-length code, we need 3 bits to represent 6 characters: a = 000, b = 001, . . . , f = 101. This method requires 300,000 bits to code the entire file.
- Using the variable-length code shown, we can encode the file in only 224,000 bits.
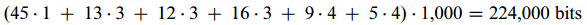 // this method achieved a saving of approximately 25% and in fact, this is an optimal character code for this file
// this method achieved a saving of approximately 25% and in fact, this is an optimal character code for this file
1.3 Prefix codes
(As the naming issue mentioned in CLRS, I do reckon that something like “prefix-free codes” might be a better name…)
A prefix code can always achieve the optimal data compression among any character code. —— CRLS
-
Encoding is always simple for any binary character code; we just concatenate the codewords representing each character of the file.
- we code the 3-character file: “abc” as
0.101.100 = 0101100, where “.” denotes concatenation.
- we code the 3-character file: “abc” as
-
Prefix codes are desirable because they simplify decoding ! Since no codeword is a prefix of any other, the codeword that begins an encoded file is unambiguous.
- By unambiguous, I mean we can simply identify the initial codeword, translate it back to the original character, and repeat the decoding process on the remainder of the encoded file.
- the string
001011101parses uniquely as0.0.101.1101, which decodes to"aabe".
1.4 Decoding representation
The decoding process needs a convenient representation for the prefix code so that we can easily pick off the initial codeword. A binary tree whose leaves are the given characters provides one such representation. —— CRLS
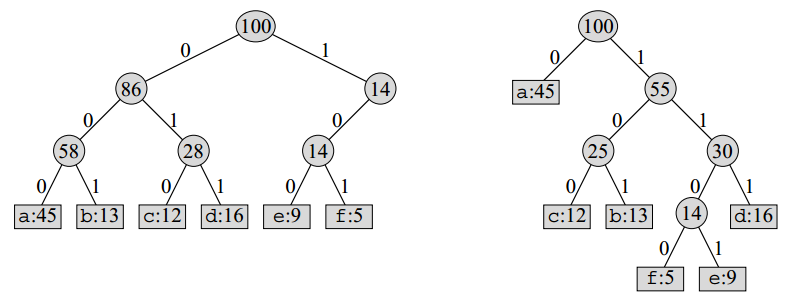
Interpretation:
- A simple path from the root to a character: a codeword for a character
- 0: go to the left child
- 1: go to the right child
Tip: note that these trees are not BSTs as their leaves need not appear in sorted order, and internal nodes do not contain character keys.
1.5 Optimal code properties
An optimal code for a file is always represented by a full binary tree, in which every non-leaf node has two children. —— CRLS
Therefore, the fixed-length code in the figure is not optimal since its tree is not a full binary tree: it contains codewords beginning with 10. . ., but not beginning with 11. . ..
Binary tree (BT) properties for prefix coding:
-
BT must be full;
-
If
Cis the alphabet from which the characters are drawn, all character frequencies are positive; -
The tree for an optimal prefix code has exactly
|C|leaves, one for each letter of the alphabet; -
The tree has exactly
|C| - 1internal nodes; -
Given a tree
Tcorresponding to a prefix code, we can easily compute the number of bits required to encode a file as follows- let’s denote
cas each character in the alphabetC; c.freqdenotes the frequency ofcin a file;d_T(c)denotes the depth of thec’s leaf inT; ( Note thatd_T(c)is also the length of the codeword for characterc)- The number of bits required to encode a file is thus ( the cost of the tree ):
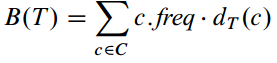
- let’s denote
2. Huffman encoding
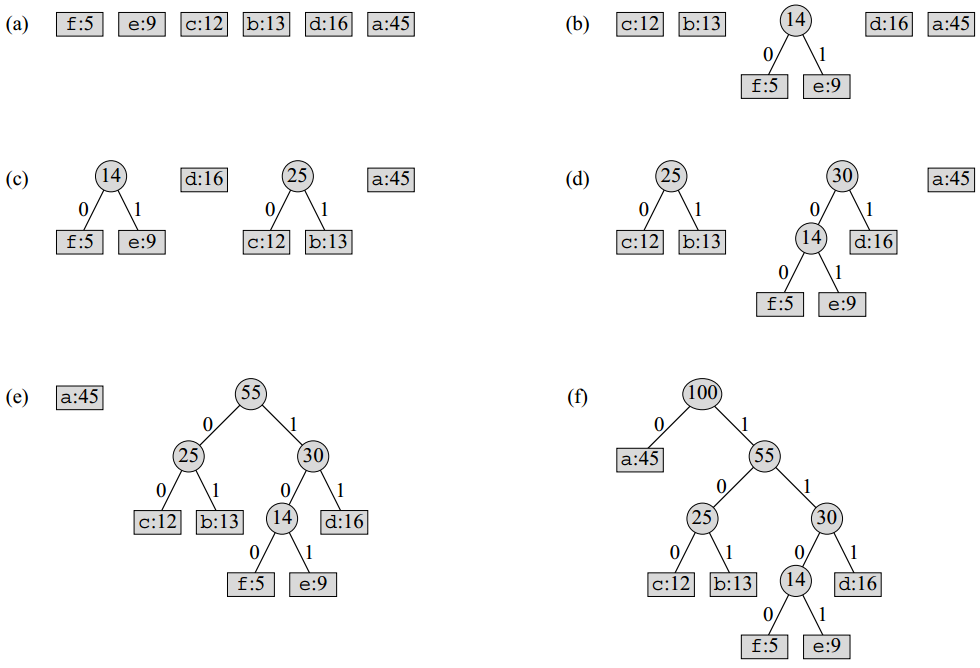
2.1 Pseudocode
struct CharNode {
char value;
int freq;
CharNode* left;
CharNode* right;
};
C = Set[CharNode]
Algorithm HuffmanEncoding(C):
n := |C|
Q := new MinPriorityQueue( BuildMinHeap(C, key=freq) )
For i := 1 to (n-1) do
newNode := new CharNode
newNode.left := ExtractMin(Q)
newNode.right:= ExtractMin(Q)
newNode.freq := newNode.left.freq + newNode.right.freq
MinHeapInsert(Q, newNode)
return ExtractMin(Q) --> return the root of the tree
-
Huffman encoding builds a tree T corresponding to the optimal code in a bottom-up manner. It begins with a set of
|C|leaves and performs a sequence of|C| - 1“merging” operations to create the final tree. (n-1times merging). -
The algorithm uses a min-priority queue
Qkeyed on thefreqattribute in order to to identify the two least-frequent node objects to merge together. -
When we merge two nodes (setting the
leftandrightfor thenewNode), the result is a new node whose frequency is the sum of the frequencies of the two nodes that were merged.
2.2 Time Complexity
BuildMinHeap()in $O(n)$ time;- The for-loop has (n-1) iterations;
ExtractMin()andMinHeapInsert()in $O(lgn)$ time carrying on by the for-loop (n-1) times; ( recall each heap modification operation is in $O(lgn)$ )
Tips: We can reduce the running time to \(O(nlglgn)\) by replacing the binary min-heap with a van Emde Boas tree (see CRLS Chapter 20).

Leave a comment