AVL Search Tree
Updated:
⚠️ This post was created when I was in high school and is no longer maintained.
(Adel’son-Vel’skii & Landis 1962)
1. Recap tree basics and BST
-
Height of node = length (# edges) of longest downward path to a leaf (see CLRS B.5 for details).
-
BSTs support
insert,delete,min,max,next-larger(successor),next-smaller(predecessor), etc. in O(h) time, where h = height of tree (= height of root). -
Why being balanced matters?
- Height h is between log~2~n and n
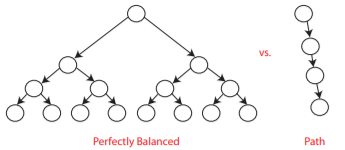
- Height h is between log~2~n and n
(“The unlucky case”: Build a BST from a sorted arrary)
- balanced BST maintains `h = O(lg n)` ⇒ all operations run in `O(lg n)` time
2. AVL Tree
We want to have as many nodes and smaller height as possible for a tree structure.
2.1 Data structure augmentation
- AVL∈ BST∈ BT
- each node also stores its height (or just difference in heights)
- treat
NILnode as height -1
2.2 AVL property
For every node, require the heights of right and left children to differ at most |1|
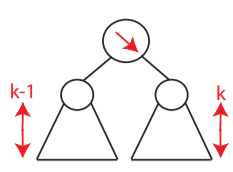
2.3 Worst-case
Worst-case occurs when the height of every node differs by 1.
let N_h be the minimum number of nodes in an AVL tree of height h:

Tips:
2^{h/2}: the number of time we multipleN_{h-2}by 2 equals to how many times we can subtract 2 fromh;- How many times can we subtract 2 from
h? - h/2 times ***
3 AVL operations
3.1 Insertion
Loop invariant: (Assume x is the lowest node violating the AVL property and assume x is “too right-heavy”)
- case 1 [same-direction-heavy]: x’s right child is also right-heavey or balanced
- We reversely rotate x (LeftRotate(x)):
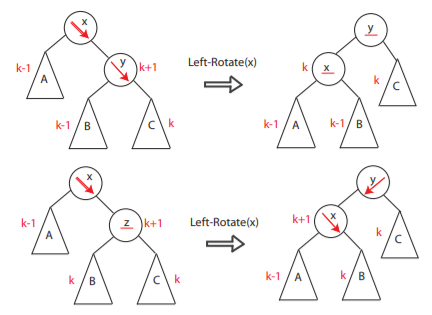 Tips: If X is too right-heavy and X’s right child Y is right-heavy or balanced, then after
Tips: If X is too right-heavy and X’s right child Y is right-heavy or balanced, then after Left-Rotate(X), X will take the “lighter” child of Y as its own child which will be no longer “too right-heavy”. (replace X’s “too heavy” right child Y by Y’s “light child”) - Then continue doing so up to x’s grandparent, great grandparent …
- We reversely rotate x (LeftRotate(x)):
- case 2 [Z-shap-heavy]: if the heavy child node of x and z (x’s heavy child) are in a different directory -> x’s right child z is left-heavy
- Rotate z to make its children heavy or too heavy in a way that its heavy node has the opposite directory as x’s heavy child (z) does. (
RightRotate(z)) - We reversely rotate x as we did in case 1
- Then continue doing so up to x’s grandparent, great-grandparent . . .
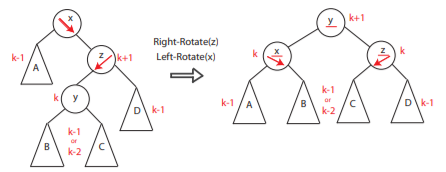
- Rotate z to make its children heavy or too heavy in a way that its heavy node has the opposite directory as x’s heavy child (z) does. (
AVL insertion steps sum up:
- insert new node using an algorithm for BST
- identify the lowest unbalanced node on the path from the new node to the root
- rebalance that node using a single or double rotation then the balance is restored
- We need at most 1 rebalance step; insertion operation is in
O(log n)
Tips:
-
What
XXRotate(node)does is to add on a layer to the lighter branch of that node. For instance, if nodexis too right-heavy, then after carrying on aleftRotate(x),x’s light branch, its left child, will be added on a new layer that comes from its heavy branch, which will makexno longer right-heavy; -
To handle the Z-shape-unbalance case, what illustrated above is to first turn this case into normal same-direction-unbalance case
-
Right-Rotate(Z) will make the left-heavy AVL tree rooted at Z become a “right-heavy or too right-heavy” tree rooted Y. Then, we use Left-Rotate(X) to let X take the “lighter” children of Y.
Examples:

3.2 Removal
Steps:
- remove node using the algorithm for BST
- consider the first unbalanced node on the path from the removed node upwards
- rebalance by considering the ‘heaviest child’ of the unbalanced node
- then, if necessary, consider the next unbalanced node and iterate rebalancing
- 6 possible cases of unbalanced nodes after update:
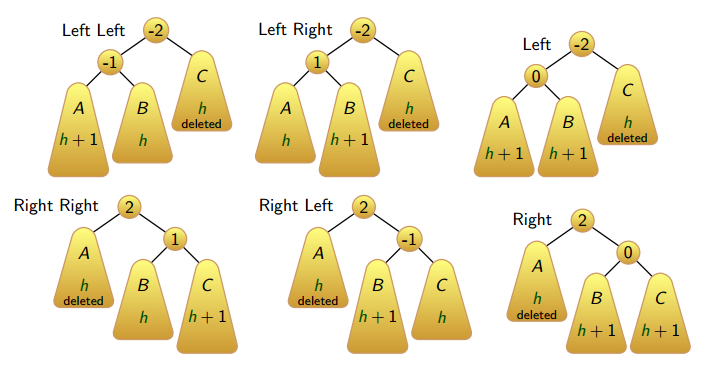
ps. we do not need more rules for rebalancing because removal is in O(log n)
3.3 Final notes concerning the differences between the insertion and removal operations
The removal operation in an AVL is generally much more hassle than insertion for the following reasons:
- removal will change the height of the tree which will possibly break the AVL property.
- consequently, after removal, checking AVL property in a bottom-up manner is needed;
- then, we recursively rebalance the unbalanced parents;
- therefore, the
deleteoperation per se is inO(logn)and therebalanceoperation is also inO(logn), so unlike the insertion which is “purely” inO(logn), it will be more precise to say that the removal is in2 * O(logn). (Well, asymptotically speaking, this does not really matter)
3.4 Time complexty


Leave a comment