Rod Cutting (DP Intro)
Updated:
⚠️ This post was created when I was in high school and is no longer maintained.
1.1 general
Dynamic programming applies when the subproblems overlap—that is when subproblems share subsubproblems
1.2 DP vs. Divide and Conquer
In DP context, a divide-and-conquer algorithm does more work than necessary, repeatedly solving the common subsubproblems.
2. Rod cutting
2.1 Problem basics
price vector:

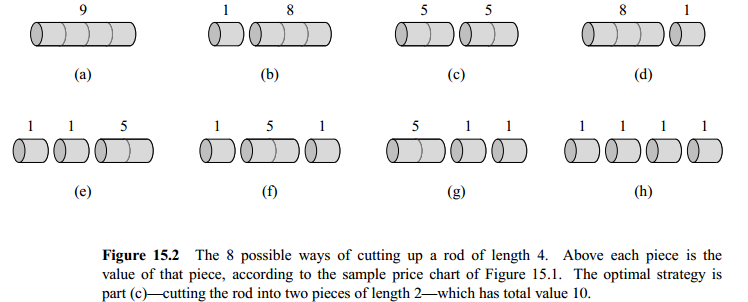
We can cut a rope in 2^n-1^ ways. (Think of a rob as an n-digit sequence of binary numbers, in which 1 represents a cut point whilst 0 represents no cuts)
What we want is to get the maximum revenue:
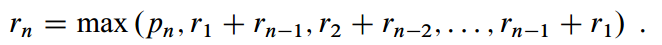
- pn: Making no cuts at all and selling the rod of length n as is.
- Other (n-1) arguments to max: By making an initial cut of the rod, we separate it into two pieces of size n and (n-i), and then optimally (recursively) cutting up those pieces further.
[Optimal structure]:
first piece + recursively optimal cutting remainder
2.2 Recursive brute-force
In the formulation below, an optimal solution embodies the solution to only one related subproblem—the remainder—rather than two.
-- @prices: the price vector --
algorithm RodCut(prices, len):
if len == 0 then
return 0
revenue := -inf
For i:= 1 to len do
-- after the for-loop, we will get the combination of the
-- cut-points by trying every different "first cut" of length `len` in each recursion,
-- and what `Max()`does is to make sure that the return value is the optimal solution --
revenue = Max(revenue, price[i]+RodCut(prices, len-i))
return revenue
2.3 Time complexity of recursive brute-force:
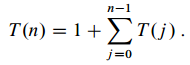 T(n) equals the number of nodes in a subtree whose root is labeled n in the recursion tree.
T(n) equals the number of nodes in a subtree whose root is labeled n in the recursion tree.
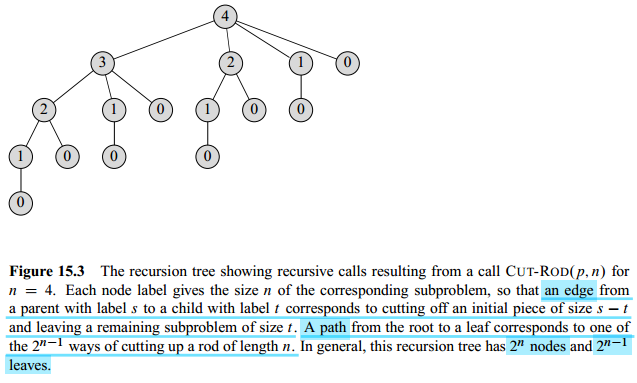
#Tree nodes == #leaves * 2 => T(n) = 2^n-1^ * 2 = 2^n^
3. DP solution for Rod cutting
3.1 Top-down with memorization
In this approach, we write the procedure recursively in a natural manner, but modified to save the result of each subproblem (usually in an array or hash table).
Intuition: In this method, as the recursive solution, we start from the top of the recursion tree (root), then we go all the way down to the leftmost leaf and store the value that we compute, which is the longest path in the tree. (We can think of this as a DFS.) As a result, at the time we back to the root and ready to start a new DFS path, we already have every value in the stock (the hash table). The only thing we need to do in the coming recursion is to look up the table and return the precomputed value. In other words, the following operations are free (constant time), so we can cut them off, which makes the tree only remains the leftmost, longest path (collapse).
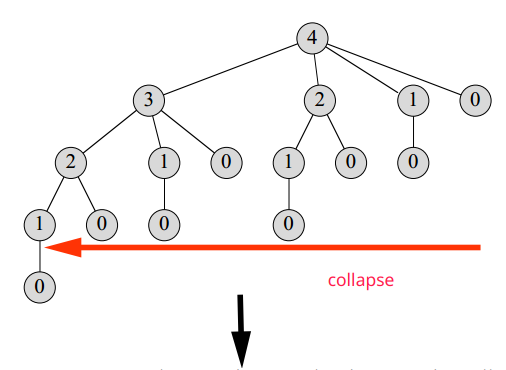
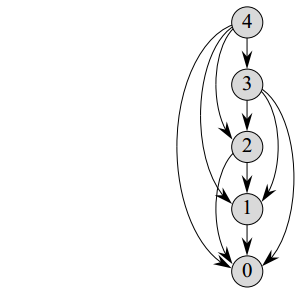
algorithm MemorizedCutRod(priceTable, len):
-- the hash table below will "remember" the optimal maxSoFar that we can achieve for len = 0 ~ len --
new optimalRevenues[0 ~ n]
For i := 1 to len:
optimalRevenues[i] := -INF
return MemorizedCutRodAux(priceTable, len, optimalRevenues)
algorithm MemorizedCutRodAux(priceTable, len, optimalRevenues):
if optimalRevenues[len] >= 0 then
return optimalRevenues[len]
if len == 0 then
maxSoFar := 0 --> base case
else
maxSoFar := -INF
For i := 1 to len do
maxSoFar = Max(maxSoFar, priceTable[i]+MemorizedCutRodAux(priceTable, len-i, optimalRevenues))
optimalRevenues[len] = maxSoFar --> memorization
return maxSoFar
Tip:
-
the
optimalRevenues[len]stores the maximum value that we can obtain when the rope has lengthlen. -
Clearly, as the nested for-loop imply, the T(n) of this DP method is O(n2) which is polynomial and is better than the recursive one where the T(n) is exponential
3.2 Bottom-up method
This approach typically depends on some natural notion of the “size” of a subproblem, such that solving any particular subproblem depends only on solving “smaller” subproblems. We sort the subproblems by size and solve them in size order, smallest first. When solving a particular subproblem, we have already solved all of the smaller subproblems its solution depends upon, and we have saved their solutions. We solve each subproblem only once, and when we first see it, we have already solved all of its prerequisite subproblems.
Intuition: In this approach, we work the way up from the leftmost leaf to the root. In a nutshell, this does exactly the same amount of computations as the top-down method does but in reverse order.
algorithm BottomUpRodCut(prices, len):
let maxRevenueTable[0~n] be a new array;
maxRevenueTable[0] = 0
-- solve smaller problems (size j) and its subproblems (size i, from 1~j) first --
For j := 1 to len:
maxRevenueSoFar := -INF
For i := 1 to j do:
maxRevenueSoFar = Max(maxRevenueSoFar, prices[i] + maxRevenueTable[j-i]) --> recall the optimal structure in section 2.1
maxRevenueTable[i] = maxRevenueSoFar
return mem_table[len]
Intermezzo: Solution Reconstruction
algorithm BottomUpRodCut(prices, len):
let mem_table[0~n] and cut_points[0~n] be a new array;
mem_table[0] = 0
cut_points[0] = 0
For j := 1 to len:
maxRevenueSoFar := -INF
For i := 1 to j do:
maxRevenueSoFar = Max(maxRevenueSoFar, prices[i] + BottomUpRodCut(prices, mem_table[j-i]))
mem_table[i] = maxRevenueSoFar
cut_point[j] = i
return mem_table, cut_point --> using these two array reconstruct the intact solution
4 Time complexity of DP
T(n) == (1 + len) * len / 2 = O(len^2^) -> O(n^2^)

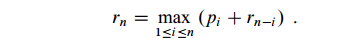
Leave a comment