Binary Search Tree (BST)

⚠️ This post was created when I was in high school and is no longer maintained.

1. Binary search recap

algorithm BinarySearch(A, key, start, end):
    if start < end then
        mid := floor((start + end) / 2)
        if key == A[mid] then
            return mid
        if key < A[mid] then
            BinarySearch(A, key, start, mid-1)
        if key > A[mid] then
            BinarySearch(A, key, mid+1, end)

=> Binary search takes Θ(log~2~n) time

---

2. Intuition

2.1 Components of a BST

- Two values: `key` and `satellite data`
- Three pointers: `left`, `right`, `parent`  ![ccf68e7ad840ffd79b66e50d142fa114.png](https://hongyuhe.github.io/_resources//25d79aa449f64240b8843edce1b9400b.png)

2.2 BST property

Tips: A BST is not necessarily an almost complete binary tree.

---

3. BST operations

3.1 Searching

TREE-SEARCH: Returns a pointer to a node with key k if one exists; otherwise, returns NIL. The procedure starts at the root and traces a path downward, comparing k with each node’s key.

{- @x: starting node
 - @k: target key
 -}
-- recursive version --
algorithm TreeSearch(x, k) 
    if x == NIL or x.key == k then
        return x
    if k < x.key then
        TreeSearch(x.left, k)
    else
        TreeSearch(x.right, k)

-- iterative version --
algorithm TreeSearch(x, k):
    While x != NIL and x.key != k do
        if k < x.key then
            x = x.left
        else 
            x = x.right
    return x

Tip: in TreeSearch(), the sequence of nodes encountered forms a simple path downward from the root.

3.2 Minimum and Maximum:

We can always find an element in a binary search tree whose key is a minimum by following left child pointers from the root until we encounter a NIL —— CRLS

-- we assume that the input node is non-NIL --
algorithm TreeMinimum(x):
    While x.left != NIL do
        x = x.left
    return x

algorithm TreeMaximum(x):
    While x.right != NIL do
        x = x.right
    return x

3.3 Successor and Predecessor

The structure of a binary search tree allows us to determine the successor/predecessor of a node without ever comparing keys. ——　CRLS

• Successor:

  If all keys are distinct, the successor of a node x is the node with the smallest key greater than x.key

In the above diagram, the inorder successor of 8 is 10, the inorder successor of 10 is 12 and inorder successor of 14 is 20.

• Predecessor:

  If all keys are distinct, the predecessor of a node x is the node with the greatest key smaller than x.key

algorithm TreeSuccessor(x):
-- there are two cases --
{-  1. node x has the right subtree:
 - find the smallest node in its right subtree 
 -}
    if x.right != NIL then 
        return TreeMinimum(x.right)
    
{-  2. node x doesn't have right subtree:
 - find the *lowest* ancestor of x whose left child 
 - is x. 
 -}
    y := x.parent
    While y != NIL and x == y.right do
    --> (once x is no longer the right child of y, x > y)
        x = y
        y = y.parent

algorithm TreePredecessor(x):
    -- the opposite --

Final notes:

• Recall that every node is its ancestor.
• The worst-case relies on the height of the tree (height matters).

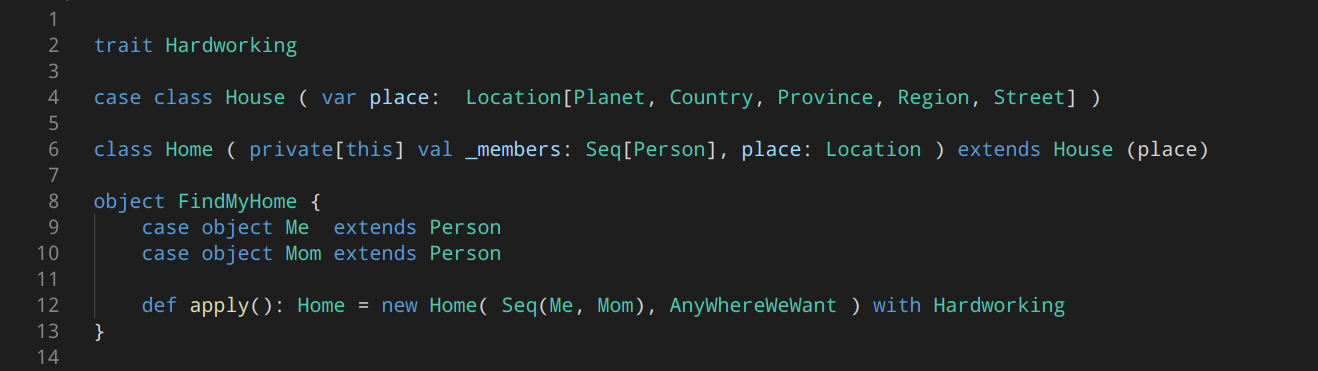
3.4 Insertion

BST insertion is nothing but fnding a correct leaf place (NIL) for the newly inserted node:

{-  Assume keys are distinct and n is the new node that need inserting 
 - with z.key = v and z.left == z.right == NIL 
 -}
algorithm TreeInsert(T, n):
    trailing := NIL --> y (in the book) is the trailing pointer that represnts the parent of x
    target   := T.root
    While target != NIL do --> Newly inserted node is always a leaf so we need to find a proper NIL for it
        trailing := target
        if n.key < target.key then 
            target = target.left
        else
            target = target.right
    n.parent := traling --> this is where the trailing pointer comes into play (set the parent pointer of the new node)
    
    if trailing == NIL then --> empty tree
        T.root = n
    else if n.key < trailing.key then
        trailing.left = n
    else 
        trailing.right = n

[Question]: why do we need a trailing pointer?

… This NIL occupies the position where we wish to place the input item n. We need the trailing pointer y because by the time we find the NIL where n belongs, the search has proceeded one step beyond the node that needs to be changed. —— CLRS

“One step beyond” means a NIL node cannot give us its parent, which we need to set n.parent (just like singly linked lists). The trailing pointer tracks the parent during the search.

3.5 Deletion

There are 3 cases:

Sum up: (say z is the node that is wanted to be deleted) If z has:

• one child / single child: replace the deleted node by NIL or its child directly; -> situation: (a), (b)
• two children:
  1. first, we need to find z’s successor node y which must be in the right subtree of z; (tips: y has no left child <- PBC see my book notes)
  2. elevate y’s child to take y’s position
  3. repace z by y and give y all z’s children

This eventually boils down to find the successor of the removed node and transplant it.

{-- TRANSPLANT replaces one subtree as a child of its
  - parent with another subtree. When TRANSPLANT replaces
  - the subtree rooted at node 'old' with the subtree
  - rooted at node 'new', node 'old'’s parent becomes node
  - 'new'’s parent, and 'old'’s parent ends up having 
  - 'new' as its appropriate child.
  -}
algorithm Transplant(T, old, new):
    -- 'old' is the root --
    if old.parent == NIL then --> Why not old == T.root? 
        T.root = new
    -- set parent node --
    else if old == old.parent.left then
        old.parent.left = new
    else 
        old.parent.right = new
    -- set parent pointer --
    if new != NIL then
        new.parent = old.parent
        
---------------------------------------

algorithm TreeDelete(T, z):
    -- case (a), (b): single child --
    if z.left == NIL then
        Transplant(z, z.right) 
    else if z.right == NIL then
        Transplant(z, z.left) --> replace directly (assume all subtrees satisfy BST property)
    else 
    -- case (c), (d): two children --
        successor := TreeMinimum(z.right) --> y 
        if successor.parent != z then
        -- case d (prepare successor) --
            Transplant(T, successor, successor.right)
            -- update right child --
            successor.right = z.right 
            successor.right.parent = successor
        
    -- case c, d (replace z by its successor) --
        Transplant(T, z, successor)
        -- update left child --
        successor.left = z.left
        successor.left.parent = successor
        

Tips: the most time-consuming procedure lies in the TreeMinimum() which may take Θ(logn) time.

---

4. Time Complexity

1. All TreeSearch() TreeMinimum() TreeMaximum() TreeSuccessor() TreePredeseccor() take O(h) time on a binary search tree of height h.

2. For TreeDelete(), Tranplant() takes constant time only TreeMinimun() takes O(h) time, so both TreeInsert() and TreeDelete() take O(h) time on a binary search tree of height h.

---

5. Intermezzo: How many BT with n nodes exist?

first Catalan numbers: 1; 1; 2; 5; 14; 42; 132; 429; 1430; 4862; 16796; 58786; 208012; 742900; 2674440; 9694845; 35357670; 129644790; 477638700; 1767263190; 6564120420; 24466267020; 91482563640; 343059613650; 1289904147324; 4861946401452; …